Maxwell’s equations

Maxwell’s equations are four fundamental equations formulated by James Clerk Maxwell that represent the basis of classical electromagnetism, dictating the design of modern communication technologies and other electromechanical systems. These equations describe how electric and magnetic fields are altered by each other and sourced by charges and currents, offering indispensable mathematical insights into a wide range of physical phenomena. This blog post will explore these equations in depth, examining their various forms, and delve into their diverse applications in modern technology and theoretical physics.

A first glance at Maxwell’s equations

    Definitions
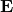  • \mathbf{E} – electric fields, 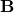\mathbf{B} – magnetic field
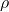  • \rho – charge density, 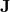\mathbf{J} – current density
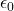  • \epsilon_0 – vacuum permittivity, 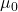\mu_0 – vacuum permeability

    1. Gauss’s law
    • Differential form: \nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0}
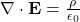
    • Integral form: \oint_S \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{enc}}{\epsilon_0}
    This law forms the basis of understanding how charge distributions produce electric fields. The popular Coulomb’s law can actually be derived from this equation as it is essentially equivalent. It is fundamental in designing capacitors and electrostatic shielding, among other applications.

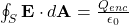
    2. Gauss’s law for magnetism
    • Differential form: \nabla \cdot \mathbf{B} = 0
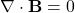
    • Integral form: \oint_S \mathbf{B} \cdot d\mathbf{A} = 0
    This law asserts the nonexistence of magnetic monopoles (a magnet will always have a north and south pole, i.e. a dipole) and is crucial in designing magnetic materials and devices. According to the differential form, the flux of a magnetic field through an enclosed surface will always be zero.

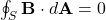
    3. Faraday’s law of induction
    • Differential form: \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}
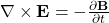
    • Integral form: \oint_C \mathbf{E} \cdot d\mathbf{l} = -\frac{d}{dt} \int_S \mathbf{B} \cdot dA
    Central to electromagnetic induction, this law explains how time-varying magnetic fields induce electric fields. It is the principle behind electric generators and transformers, forming the basis of much of today’s electrical power generation and distribution.

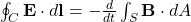
    4. Ampère’s law
    • Differential form: \nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}
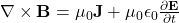
    • Integral form: \oint_C \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{enc} + \mu_0 \epsilon_0 \frac{d}{dt} \int_S \mathbf{E} \cdot d\mathbf{A}
    This law describes how electric currents and changing electric fields produce magnetic fields. It is fundamental to designing electromagnets, inductors, and understanding the magnetic effects of electric currents.

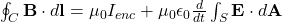
Delving deeper: Applications of Maxwell’s equations

Electromagnetic wave propagation

By combining Faraday’s law and Ampère’s law, Maxwell predicted the existence of electromagnetic waves. In other words, time and space-varying electric and magnetic fields may propagate freely through space given that the \mathbf{E} and \mathbf{B} fields are transverse to each other and the direction of wave propagation, phase shifted by \frac{\pi}{2} or 90 degrees. The electromagnetic wave equation can be derived from Maxwell’s equations as follows (using \epsilon_0 = 1 and \mu_0 = 1 for simplicity):

Derivation of the wave equation for the electric field:

Taking the curl of Faraday’s law, using a vector identity, and the fact that \nabla \cdot \mathbf{E} = 0 in a vacuum: \nabla \times (\nabla \times \mathbf{E}) = \nabla \times -\frac{\partial \mathbf{B}}{\partial t} = \nabla (\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E} = -\nabla^2 \mathbf{E}. Therefore, -\nabla^2 \mathbf{E} = \nabla \times -\frac{\partial \mathbf{B}}{\partial t}. Then, using Ampère’s law and the fact that \mathbf{J}=0 in a vacuum: \nabla^2 \mathbf{E} = \frac{\partial^2 \mathbf{E}}{\partial t^2}.

Derivation of the wave equation for the magnetic field:

Taking the curl of Ampère’s law, using a vector identity, and the fact that \mathbf{J} = 0 in a vacuum and \nabla \cdot \mathbf{B} = 0: \nabla \times (\nabla \times \mathbf{B}) = \nabla \times \frac{\partial \mathbf{E}}{\partial t} = \nabla (\nabla \cdot \mathbf{B}) - \nabla^2 \mathbf{B} = - \nabla^2 \mathbf{B}. Therefore, \nabla^2 \mathbf{B} = \nabla \times (\frac{\partial \mathbf{E}}{\partial t}) = \frac{\partial^2 \mathbf{B}}{\partial t^2} by Faraday’s law.


Notably, while both wave equations can be written solely in terms of \mathbf{E} and \mathbf{B}, respectively, a propagating electric field wave will always be accompanied by a magnetic field and vice versa. Jointly, these two equations describe the free propagation of electromagnetic waves, including visible light, which is used in LiDAR, radio waves (used in radar, Wi-Fi, and cellular signal), and other frequencies of light. It turns out that we can do a lot with electromagnetic waves. For example, by applying an AC current to an antenna, electrons are forced to oscillate and radiate radio waves into the air. This is the basic idea that underpins most wireless communication. On the other hand, the boundary conditions of electromagnetic waves incident on a material of a different refractive index provides us with Snell’s law and the Fresnel equations, dictating the refraction, reflectance, and transmission of light, especially useful for optical systems.


Post is still under construction! Up next: transformers, inductors, capacitors, and electromagnets.

1 thought on “Maxwell’s equations”

Leave a Reply

Your email address will not be published. Required fields are marked *